View on GitHub

Haskell

A mixture of Haskell quick reference guide, research logbook and tutorial full of external references

by Federico Mastellone

Evaluation Strategies

Functional programming languages extend Church’s Lambda Calculus with a variety of constructs (AKA tons of syntactic sugar) that make it useful for programmers.

The evaluation strategy determines when to evaluate argument expressions during function application. Although sometimes it looks closer to operational semantics than denotational semantics, its choice is an important element in the design of a high-level programming language.

Prelude> length [1,(1/0),3,4,5]
5
Prelude> take 5 [1,2..]
[1,2,3,4,5]

A Little Terminology

Not to be confused with λ-Calculus reduction strategies, the process by which a more complex expression is reduced to a simpler expression.

Notice that we are still not talking about the evaluation order when not constrained by operator precedence or associativity, that in languages like C is also unspecified. We are talking about how to treat expressions that need further evaluation and are used as function arguments.

In the example below by parameters we mean a and b and by arguments we mean 1 and 2*3:

add :: Int -> Int -> Int
add a b = a + b

main :: IO ()
main = print $ add 1 (2*3)

Parameter-Passing Classification

We use the classification described by Erik Crank and Matthias Felleisen in Parameter-passing and the lambda calculus where evaluation strategies are combined with the more specific notion of binding strategies that determines how values are passed to the function.

By Strictness

λ-Calculus has two prevailing semantics:

If we have this example function shown below:

const :: a -> b -> a
const a b = a

Calling const (1+1) (1/0) will return 2 in Haskell and “error” using strict semantics.

By Binding Strategy

We defined if argument expressions are evaluated before function application or not, but how is the function receiving those arguments as parameters?

Most authors refer to strict evaluation as call-by-value due to the call-by-value binding strategy requiring strict evaluation and to call-by-name as non-strict evaluation because it means that arguments are passed unevaluated to the function body, which by popular folklore is the usual Church’s lambda calculus strategy.

Confluence

With the works of Church and Rosser about reduction sequences and Plotkin about parameter-passing techniques as foundation, we know that two different reduction sequences or evaluation strategies cannot lead to different computation results (minus non-termination).

Non-termination is key. In most imperative languages different evaluation strategies can produce different results for the same program, whereas in purely functional languages the only output difference is its termination behavior.

We need a proper definition of purely functional language:

A language is purely functional if (i) it includes every simply typed λ-calculus term, and (ii) its call-by-name, call-by-need, and call-by-value implementations are equivalent (modulo divergence and errors).

A. M. R. SABRY, “What is a purely functional language?”, Journal of Functional Programming, vol. 8, no. 1, pp. 1–22, 1998.

The definition implies that a function’s return value is identical for identical arguments and the operational decision of how to pass the arguments is irrelevant. Obviously call-by-reference introduces side effects.

No wonder why Haskell and GHC do everything possible to stay true to the theory when extending lambda calculus. See Type checker and type inference in action to get an idea of what it means for the usability of the language to be pure (no side-effects), non-strict and statically typed in pursuit of safety.

Lazy vs. non-strict

If a function is non-strict, we say that it is lazy. Technically, this is an abuse of terminology, since lazy evaluation is an implementation technique which implements non-strict semantics. However, ‘lazy’ is such an evocative term that it is often used where ‘non-strict’ would be more correct.

The Implementation of Functional Programming Languages, Simon Peyton Jones, Published by Prentice Hall | January 1987

The term lazy is informally interchangeable with non-strict because it’s the prevalent implementation technique for non-strict languages, but laziness is not the only way to implement non-strictness.

Haskell’s definition

Haskell is often described as a lazy language. However, the language specification simply states that Haskell is non-strict, which is not quite the same thing as lazy:

Function application in Haskell is non-strict; that is, a function argument is evaluated only when required.

Haskell 2010 report - 6.2 Strict Evaluation.

A Haskell implementation using call-by-name would be technically conforming.

Implementation Details

GHC laziness refers to the operational semantics used to perform a call-by-need reduction. The technique is called lazy graph reduction because the expression tree becomes a graph when reusing expressions.

Its implementation details are only mentioned here: The first ingredient of call-by-need, that a function argument is evaluated only when required, is directly implemented by using a normal order reduction. The second ingredient, that once evaluated should never be re-evaluated, is implemented with a combination of two things:

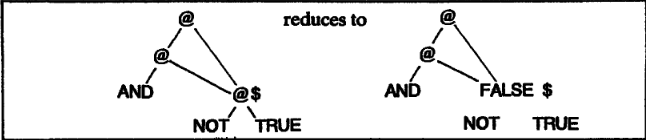
Figure 12.2 Pointer Substitution Figure 12.3 Overwriting the Root of the Redex

Memoization

Now that we know that Haskell computes any given expression at most once every time the lambda expression is entered, we can use the memoization optimization technique:

slow_fib :: Int -> Integer
slow_fib 0 = 0
slow_fib 1 = 1
slow_fib n = slow_fib (n-2) + slow_fib (n-1)

memoized_fib :: Int -> Integer
memoized_fib i = map fib [0 ..] !! i
        where fib 0 = 0
              fib 1 = 1
              fib n = memoized_fib (n-2) + memoized_fib (n-1)

Further Reading